Surface area study guide answer key – Delve into the realm of surface area with our comprehensive study guide answer key, empowering you to master the intricacies of geometric calculations. This guide unveils the significance of surface area, equips you with formulas for common shapes, and explores its diverse applications across multiple disciplines.
As we navigate through this guide, you will gain a profound understanding of surface area, its relationship with volume, and techniques for tackling irregular shapes. Our clear explanations, illustrative examples, and concise FAQs will illuminate your path to geometric mastery.
Surface Area Definition
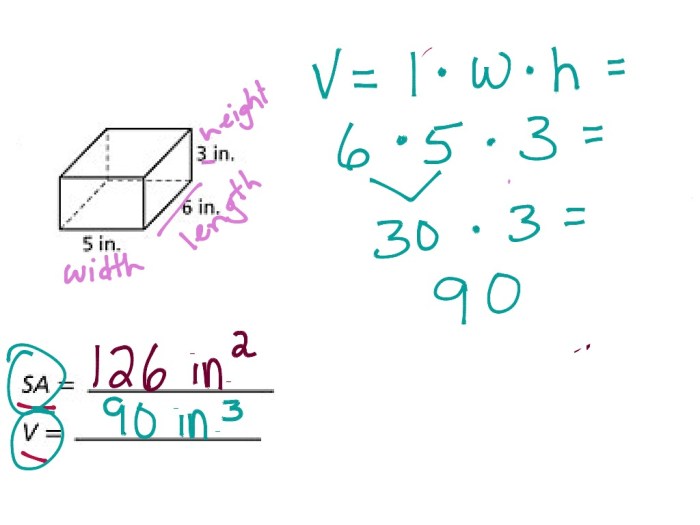
Surface area refers to the total area of all exposed surfaces of a three-dimensional object. It is a fundamental geometric property used in various scientific and engineering disciplines to determine the extent and characteristics of surfaces.
Understanding surface area is crucial in numerous fields, including architecture, engineering, physics, chemistry, and biology. It enables the calculation of surface-to-volume ratios, heat transfer rates, fluid flow dynamics, and the efficiency of chemical reactions, among other applications.
Significance of Surface Area, Surface area study guide answer key
The surface area of an object influences several important factors:
- Heat transfer:Surface area affects the rate of heat transfer through conduction, convection, and radiation.
- Fluid flow:The surface area of a body immersed in a fluid affects the drag force and the rate of fluid flow.
- Chemical reactions:The surface area of a catalyst or reactant affects the rate of chemical reactions.
- Biology:Surface area is critical in determining the exchange of nutrients and gases in living organisms, such as through the lungs and the digestive system.
Formulas for Surface Area
The surface area of an object is the total area of its surfaces. It is an important concept in geometry and has applications in various fields, such as engineering, architecture, and biology.
There are different formulas for calculating the surface area of different shapes. Some of the most common shapes and their surface area formulas are given in the table below:
| Shape | Formula |
|---|---|
| Cube | 6s2 |
| Sphere | 4πr2 |
| Cylinder | 2πrh + 2πr2 |
In these formulas, s represents the length of the side of the cube, r represents the radius of the sphere or cylinder, and h represents the height of the cylinder.
Applications of Surface Area
Surface area finds applications in various fields, including architecture, engineering, and biology. Understanding the surface area of objects is essential for designing efficient structures, optimizing processes, and studying biological phenomena.
Architecture
- Building design:Surface area determines the amount of materials needed for construction, the energy required for heating and cooling, and the natural lighting available within a building.
- Roofing:The surface area of a roof is crucial for calculating the amount of roofing materials required and estimating the cost of roofing.
- Ventilation:Surface area influences the rate of air exchange within a building, affecting indoor air quality and energy efficiency.
Engineering
- Heat transfer:Surface area plays a vital role in heat transfer processes, such as conduction, convection, and radiation. It determines the rate at which heat is transferred between objects.
- Fluid dynamics:The surface area of objects immersed in fluids affects the drag force and lift experienced by the objects.
- Chemical reactions:Surface area is a crucial factor in chemical reactions that occur on surfaces, such as heterogeneous catalysis.
Biology
- Cellular respiration:The surface area of cells influences the rate of cellular respiration, as it determines the amount of oxygen that can diffuse into the cells.
- Gas exchange:The surface area of lungs and gills is crucial for gas exchange, as it determines the rate of oxygen and carbon dioxide exchange between the organism and its environment.
- Diffusion:Surface area affects the rate of diffusion of substances across membranes, such as the cell membrane.
Surface Area of Irregular Shapes
Irregular shapes do not have a defined formula for calculating their surface area. However, there are several methods for estimating the surface area of irregular shapes.One common method is triangulation. Triangulation involves dividing the irregular shape into a series of triangles.
The surface area of each triangle can then be calculated using the formula for the area of a triangle:“`A = (1/2)
- b
- h
“`where:* A is the area of the triangle
- b is the base of the triangle
- h is the height of the triangle
Once the surface area of each triangle has been calculated, the total surface area of the irregular shape can be found by adding the surface areas of all the triangles.Another method for estimating the surface area of irregular shapes is to use a grid.
A grid is a pattern of squares or rectangles that is superimposed over the irregular shape. The surface area of the irregular shape can then be estimated by counting the number of squares or rectangles that overlap the shape.The accuracy of the surface area estimate will depend on the size of the grid.
A smaller grid will provide a more accurate estimate, but it will also be more time-consuming to use.
Example of Using Triangulation
Consider an irregular shape that can be divided into two triangles. The base of the first triangle is 5 cm and its height is 3 cm. The base of the second triangle is 4 cm and its height is 2 cm.Using
the formula for the area of a triangle, we can calculate the surface area of each triangle:“`A1 = (1/2)
- 5 cm
- 3 cm = 7.5 cm^2
A2 = (1/2)
- 4 cm
- 2 cm = 4 cm^2
“`The total surface area of the irregular shape is the sum of the surface areas of the two triangles:“`A = A1 + A2 = 7.5 cm^2 + 4 cm^2 = 11.5 cm^2“`Therefore, the estimated surface area of the irregular shape is 11.5 cm^2.
Surface Area and Volume
Surface area and volume are two fundamental geometric properties of three-dimensional objects. They are closely related, and understanding their relationship is essential for many applications in science and engineering.
The surface area of an object is the total area of its surfaces. The volume of an object is the amount of space it occupies. In general, the surface area of an object increases as its volume increases. This is because as an object gets larger, it has more surfaces.
Examples of the Relationship between Surface Area and Volume
- A cube with a side length of 1 has a surface area of 6 and a volume of 1.
- A cube with a side length of 2 has a surface area of 24 and a volume of 8.
- A cube with a side length of 3 has a surface area of 54 and a volume of 27.
As you can see from these examples, the surface area of a cube increases as the cube’s volume increases. This is true for all three-dimensional objects.
Surface Area of Prisms and Pyramids: Surface Area Study Guide Answer Key
Prisms and pyramids are three-dimensional shapes with flat faces. The surface area of a prism or pyramid is the sum of the areas of all its faces.
To calculate the surface area of a prism, we need to know the area of each face and the number of faces. The faces of a prism are rectangles or triangles. To find the area of a rectangle, we multiply the length by the width.
To find the area of a triangle, we multiply the base by the height and divide by 2.
Once we have the area of each face, we can find the surface area of the prism by adding up the areas of all the faces.
Surface Area of Pyramids
To calculate the surface area of a pyramid, we need to know the area of the base and the area of each triangular face. The base of a pyramid is a polygon, which can be a triangle, square, rectangle, or other shape.
To find the area of the base, we use the same formulas as we would for finding the area of any other polygon.
To find the area of a triangular face, we multiply the base by the height and divide by 2. Once we have the area of the base and the area of each triangular face, we can find the surface area of the pyramid by adding up the areas of all the faces.
Surface Area of Spheres and Cones
In this section, we will explore the formulas and methods for calculating the surface area of spheres and cones. Understanding these concepts is crucial in various fields, including geometry, engineering, and physics.
Surface Area of Spheres
A sphere is a three-dimensional shape with all points equidistant from a fixed central point. The surface area of a sphere is the total area of its curved surface.
The formula for the surface area of a sphere with radius ris given by:
$$A = 4\pi r^2$$
Surface Area of Cones
A cone is a three-dimensional shape with a circular base and a single vertex. The surface area of a cone consists of the area of the circular base and the area of the cone’s curved surface.
The formula for the surface area of a cone with radius r, height h, and slant height lis given by:
$$A = \pi r^2 + \pi rl$$
where:
- Ais the surface area of the cone
- ris the radius of the circular base
- his the height of the cone
- lis the slant height of the cone
Frequently Asked Questions
What is the formula for the surface area of a sphere?
4πr², where r is the radius of the sphere.
How can I calculate the surface area of an irregular shape?
Use triangulation or other techniques to approximate the shape as a combination of regular shapes, then calculate the surface area of each part and add them together.
What is the relationship between surface area and volume?
Surface area is directly proportional to volume for similar shapes, meaning that as volume increases, surface area also increases.
