Assume that segments that appear to be tangent are tangent, a fundamental principle in geometry, opens a gateway to understanding the intricacies of geometric relationships. This assumption forms the cornerstone of geometric calculations and constructions, shaping the world of shapes and angles.

Throughout this discourse, we will delve into the mathematical definition of tangency, explore the criteria for identifying tangent segments, and unravel the implications of this assumption on geometric constructions and theorems. We will also examine historical perspectives, related concepts, and exceptions to this rule, providing a comprehensive understanding of this foundational principle.

Tangency Definition

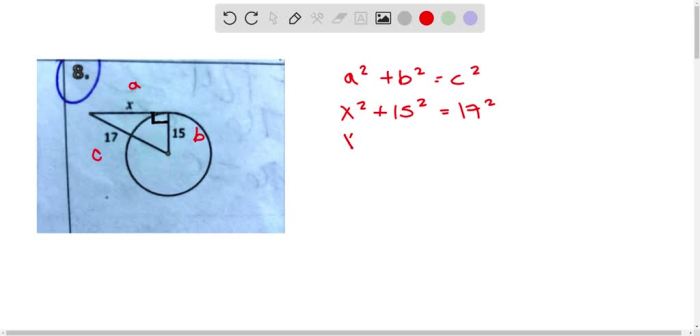
In geometry, tangency refers to the unique point of contact between two geometric objects. Tangency can occur between two lines, two circles, or a line and a circle.

Mathematical Definition

Formally, two geometric objects are said to be tangent if they intersect at exactly one point and share a common tangent line at that point.

Tangent Lines and Tangent Circles

A tangent line is a line that intersects a circle at exactly one point. A tangent circle is a circle that intersects another circle at exactly one point.

Identifying Tangent Segments

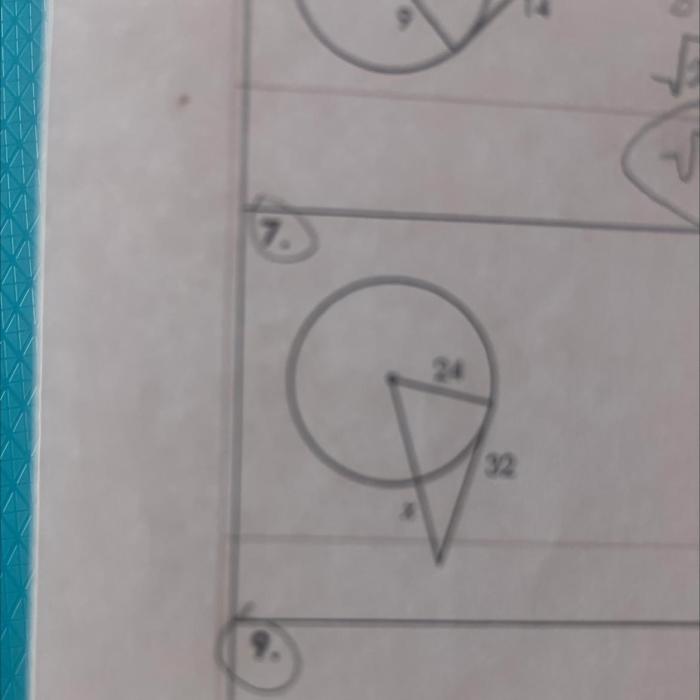
Determining whether segments are tangent can be done by examining their relative positions and orientations.

Conditions for Tangency

• The segments must intersect at exactly one point.
• The segments must be on opposite sides of the point of intersection.
• The segments must not cross each other at any other point.

Examples in Real-World Applications, Assume that segments that appear to be tangent are tangent

• The spokes of a bicycle wheel are tangent to the rim.
• The edges of a square are tangent to the inscribed circle.

Implications of Tangency

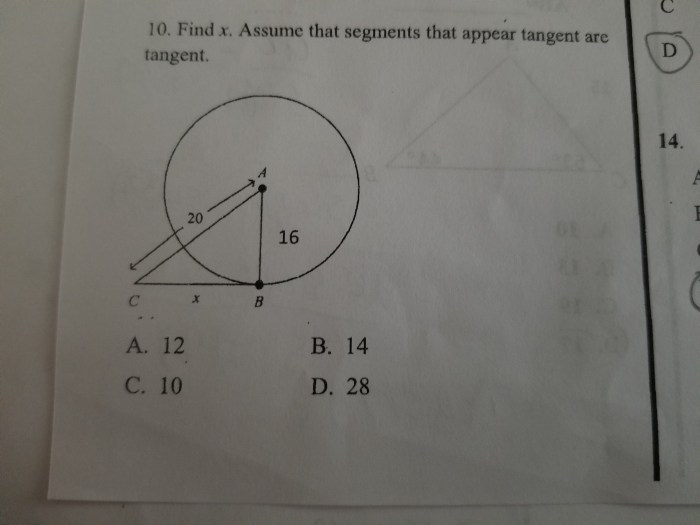
Assuming that segments are tangent has significant implications for geometric calculations and constructions.

Impact on Geometric Calculations

• Tangent segments can be used to determine the lengths of other segments.
• Tangent segments can be used to find the radii of circles.

Impact on Geometric Constructions

• Tangent segments can be used to construct tangent lines and circles.
• Tangent segments can be used to divide angles into equal parts.

Applications in Geometry: Assume That Segments That Appear To Be Tangent Are Tangent

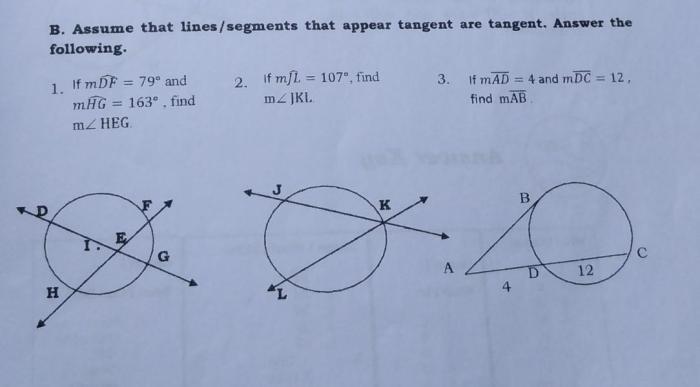
Tangency is a fundamental concept in geometry and is used in numerous theorems and constructions.

Geometric Theorems

• Tangent circles theorem: The common tangent segments to two circles are equal in length.
• Angle bisector theorem: The angle bisector of a triangle is tangent to the incircle.

Geometric Constructions

• Constructing a tangent line to a circle from an external point.
• Constructing a circle tangent to two given lines.

Exceptions and Limitations

While tangency is a useful assumption in many geometric situations, there are exceptions where it may not be valid.

Invalid Assumptions

• Segments that appear to be tangent may not actually be tangent.
• Segments that are tangent in one situation may not be tangent in another.

Consequences of Incorrect Assumptions

• Incorrect assumptions can lead to incorrect geometric calculations.
• Incorrect assumptions can make geometric constructions impossible or inaccurate.

FAQ Resource

What is the mathematical definition of tangency?

Tangency occurs when a line or curve touches another line or curve at a single point, without crossing it.

How can we identify tangent segments?

Tangent segments can be identified when they share a common endpoint and lie on opposite sides of the tangent line or circle.

What are the implications of assuming segments are tangent?

Assuming segments are tangent allows us to make geometric deductions and constructions based on the properties of tangent lines and circles.